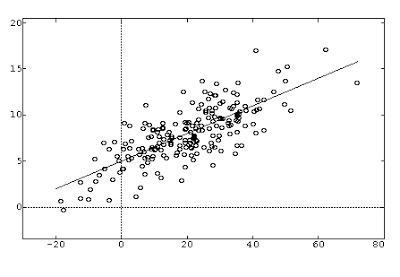
linear regression

Following is taken from a conversation I had with an MBA student whose background was engineering.

MBA: People at this business school mistake linear regressions for models. When I was in college, we used to analytically solve complicated differential equations in order to model motions of various systems. That was some advanced mathematics, some real modelling... This regression stuff on the other hand is a joke.

Me: Use of advanced mathematics does not imply that there is some advanced modelling going on. Sometimes the intuition required to discover a pattern will require immense amounts of intellectual effort and creativity, but the final mathematical description of this pattern will be fairly elementary. This indeed was the case with Einstein's theory of special relativity.

Complicated mathematics often lead to decreased conceptual clarity. Hence the reason why mathematicians struggle to find simpler and more conceptual proofs for results whose validity have been demonstrated via unnatural and complicated means.

You probably derived those differential equations by applying Newton's laws to not-too-complicated systems. Strictly speaking you did some modelling while choosing which assumptions to make during the simplification of the system in question. However the real modelling was done on a more basic level by Newton himself.

Newton could not have directly intuited the dynamics underlying the motion of a complicated system. Human mind does not work that way. He started out with simpler systems and modelled them first. The principles he extracted turned out to be universal and applicable to more complicated systems in a well-defined manner.

Unlike physics, macroeconomics does not lend itself to ground-up modelling. Economists have tried to aggregate models of individual level decision making processes to an aggregate level dynamical framework. None have achieved any success.

Say you have two vectors of data and you suspect that there exists some kind of a statistical dependence between them. You create a scatter-plot and look for a functional relationship between the two vectors. The technique of linear regression amounts to drawing the best fitting straight line through this data set:

You are of course free to fit anything to the data. You could try approximating it with higher degree polynomials or trigonometric series. The simplest thing to do however is to approximate it using a linear function. Remember that you do not want to over-analyze. "Is there a linear relationship?" is the humblest question you can ask to your data. A sixth degree polynomial relationship is more likely to turn out to be spurious than a linear one.

In the future, analytical solutions to tough differential equations will not be sought after by engineers. Numerical approximations given by super computers will suffice for all practical considerations. (The algorithms at work will be quite basic in comparison to the sophisticated mathematical tools employed for extracting analytical solutions.)

In a linear regression, simplicity arises due to our lack of knowledge of the interior workings of the system and due to our goal of making robust claims about the future behaviour of the system. In Newton's case, however, the source of the resulting simplicity is a mystery. Why does nature, at certain scales, behave in such a mathematically simple fashion? We do not know.